1989 gaben Martin Fleischmann und Stanley Pons eine Pressekonferenz in der sie behaupteten ihnen wäre eine kalte Fusion geglückt. Leider waren die Ergebnisse nicht (bzw nur teilweise) reproduzierbar und selbst wenn es Messungen von "excess heat" (also überschüssige Energie) gab, passten die Ergebnisse nicht zu einer Fusion von Deuterium und waren so gering, dass es sich auch um einen systematischen Fehler in der Kalorimetrie handeln könnte. Es soll in diesem Artikel aber nicht um die experimentellen Arbeiten im Detail gehen, sondern um die Theorie.
1. Einleitung
( Wer nur etwas zur Widom-Larson-Theorie lesen möchte, kann diesen Abschnitt über Fusion überspringen)
Werfen wir also erstmal einen Blick auf eine Kernfusion von Wasserstoff: $\rm{{}^2H +{}^3H \to {}^4He + {}^1n }$ Zwei Wasserstoffisotope fusionieren miteinander zu Helium und einem Neutron. Nun ist diese Gleichung aber nicht komplett, denn auf beiden Seiten der Gleichung muss wegen der Energieerhaltung die gleiche Energie stehen. Seit Einsteins berühmter Formel $E=mc^2$ wissen wir, dass wir auch auf die "Massenerhaltung" achten müssen. Auf den ersten Blick sieht das dann immer noch korrekt aus. Auf der linke Seiten haben wir 1 Proton + 1 Neutron vom ersten Wasserstoffisotop und 1 Proton + 2 Neutronen vom zweiten. Auf der rechten Seite haben wir 2 Proton + 2 Neutronen vom Helium sowie 1 Neutron. Also je zwei Protonen und drei Neutronen. Nun gibt es aber den sogenannte Massendeffekt. Ein Proton wiegt $1{,}00728~\rm{u}$ und ein Neutron $1{,}00866~\rm{u}$, also wiegen zwei Protonen und zwei Neutronen zusammen: $ 2 \cdot 1{,}00728~\rm{u} + 2 \cdot 1{,}00866~\rm{u} = 4{},03186 \rm{u}$. Helium-4 hat aber eine Ruhemasse von nur $4{,}00260~\rm{u}$. Diese Massedifferenz führt bei einer solchen Fusion oder einer vergleichbaren Deuteriumfusion, wie sie in Sternen wie unserer Sonne oder bei Wasserstoffbomben auftritt, zu den immensen Mengen frei werdender Energie. Die Energie die sich nach dem Urknall in Materie "verfestigt" hat, bietet ein immenses Potential. Das c² in $\rm{E=mc^2}$ ist ein riesiger Wert
$$
c^2 = \mathrm{(299\,792\,458 \frac{m}{s})^2 = 89\,875\,517\,873\,681\,764 \frac{m^2}{s^2}}
$$
Rechnet man also die Energie aus, die in einem Kilogramm beliebige Materie steckt, so erhält man:
$$
E = mc^2 = \mathrm{ 1~kg \cdot (299\,792\,458 \frac{m}{s})^2 = 89\,875\,517\,873\,681\,764 J \\\\= 89\,875\,517\,874~MJ = 24\,965\,421\,631~kWh }
$$
Ein Kilogramm Kohle hat im Idealfall einen Heizwert von ca 10 kWh, was verglichen zu den 25 000 000 000 kWh Energie in Form von Materie natürlich winzig ist. Die Frage ist nur, wie man an eben an diese Energie rankommt. Die "konventionelle" Atomkraft hat natürlich einen Weg, aber der Preis (Risiko eines GAUs, radioaktiver Müll) ist schlicht zu hoch. Könnte man also Wasserstoff bei "niedrigen" Temperaturen (ein paar hundert °C) ohne gefährliche Neutronenstrahlung fusionieren lassen, hätte man eine saubere Energiequelle gefunden, da kein strahlender Atommüll, sondern nur Helium entsteht.
Möchte man die etablierte Physik nicht einfach über Bord werfen, so gibt es bei den Versuchen mit Palladium-Deuterium oder Nickel-Wasserstoff-Zellen drei theoretische Probleme - oder miracles wie sie John Huizenga in seinem Buch "Kalte Kernfusion. Das Wunder, das nie stattfand" nennt:
Das größte Problem ist die Abstoßung gleicher Ladungen (Punkt 1). Zum einen stoßen sich Wasserstoff Atome durch ihre negativ "Elektronenhülle" ab und selbst wenn die Atomkerne nahe genug aneinander wären, würden auch diese sich durch ihre positiven Ladungen abstoßen. Man würde also erstmal sehr hohe Energien brauchen um die Atomekerne überhaupt mal nahe genug aneinander zu bringen. In der Sonne, einer Wasserstoffbombe oder bei einem Fusionskraftwerk wie ITER, hat man daher immense Temperaturen. In der Sonne sind Temperaturen von mehr als 3 000 000°C nötig, damit eine Proton-Proton-Reaktion zustande kommen kann. Bei derartige Temperaturen sind die Wasserstoffatome sowieso in einem vollständig ionisierten Plasma, also spielt die Abstoßung durch die Elektronenhülle keine Rolle mehr. Aber selbst dann ist es nur durch den Tunneleffekt möglich, dass eine aufrechterhaltende Fusionsreaktion zustande kommt. Um die nötige Aktivierungsenergie bei einer Wasserstoffbombe zu bekommen, wird dazu erstmal eine Kernspaltung (also eine "normale" Atombombe) gezündet und einem Fusionsreaktor des Tokamak Designs, wird das mehrere Millionen °C heiße Plasma durch ein Magnetfeld erzeugt und an der Stelle gehalten. Selbst wenn es "irgendwie" möglich wäre, eine Proton-Proton-Reaktion quasi bei Zimmertemperatur (oder ein paar hundert grad darüber), also "kalt" ablaufen zu lassen, hätte man noch das Problem, dass auch bei der Nutzbarmachung von "heißen" Fusionsreaktoren auftritt: ca 80% der freiwerdenden Energie ist nämlich kinetische Energie des entstehenden Neutrons, also Neutronenstrahlung. Gerade letztere scheint aber bei Versuchen wie die von Fleischmann und Pons gänzlich zu fehlen (Punkt 2). Außerdem müsste unter der Vielzahl der Reaktionen auch Wasserstoff zu Deuterium Reaktion wie $\rm{{}^1H + {}^1H \to {}^2H + e^+} + {\nu}_e$ ablaufen. Bei dieser Reaktion entsteht ein Positron, welches sehr schnell mit einem Elektron annihiliert wird. Dadurch enstehen zwei Photonen mit der charakteristischen Energie von $\rm{0{,}511~{MeV}}$. Diese Gammastrahlung fehlt aber ebenfalls (Punkt 3).
Aus theoretischer Sicht ist eine "kalte" Fusion also Humbug.
Was ist aber mit der vielzahl der Publikationen die "überschüßige Energie" und sogar Transmutationsprodukte in derartigen Zellen gemessen haben? Sind das nur falsch positive Ergebnisse oder gar Betrug? Was veranlasst die Zawodny von der NASA Langley zu solchen Aussagen:
$$
c^2 = \mathrm{(299\,792\,458 \frac{m}{s})^2 = 89\,875\,517\,873\,681\,764 \frac{m^2}{s^2}}
$$
Rechnet man also die Energie aus, die in einem Kilogramm beliebige Materie steckt, so erhält man:
$$
E = mc^2 = \mathrm{ 1~kg \cdot (299\,792\,458 \frac{m}{s})^2 = 89\,875\,517\,873\,681\,764 J \\\\= 89\,875\,517\,874~MJ = 24\,965\,421\,631~kWh }
$$
Ein Kilogramm Kohle hat im Idealfall einen Heizwert von ca 10 kWh, was verglichen zu den 25 000 000 000 kWh Energie in Form von Materie natürlich winzig ist. Die Frage ist nur, wie man an eben an diese Energie rankommt. Die "konventionelle" Atomkraft hat natürlich einen Weg, aber der Preis (Risiko eines GAUs, radioaktiver Müll) ist schlicht zu hoch. Könnte man also Wasserstoff bei "niedrigen" Temperaturen (ein paar hundert °C) ohne gefährliche Neutronenstrahlung fusionieren lassen, hätte man eine saubere Energiequelle gefunden, da kein strahlender Atommüll, sondern nur Helium entsteht.
Möchte man die etablierte Physik nicht einfach über Bord werfen, so gibt es bei den Versuchen mit Palladium-Deuterium oder Nickel-Wasserstoff-Zellen drei theoretische Probleme - oder miracles wie sie John Huizenga in seinem Buch "Kalte Kernfusion. Das Wunder, das nie stattfand" nennt:
- Die Frage wie die Coulomb-Barriere überwunden wird
- Die fehlende Neutronenstrahlungs
- Die fehlende Gamma oder Röntgenstrahlung
Das größte Problem ist die Abstoßung gleicher Ladungen (Punkt 1). Zum einen stoßen sich Wasserstoff Atome durch ihre negativ "Elektronenhülle" ab und selbst wenn die Atomkerne nahe genug aneinander wären, würden auch diese sich durch ihre positiven Ladungen abstoßen. Man würde also erstmal sehr hohe Energien brauchen um die Atomekerne überhaupt mal nahe genug aneinander zu bringen. In der Sonne, einer Wasserstoffbombe oder bei einem Fusionskraftwerk wie ITER, hat man daher immense Temperaturen. In der Sonne sind Temperaturen von mehr als 3 000 000°C nötig, damit eine Proton-Proton-Reaktion zustande kommen kann. Bei derartige Temperaturen sind die Wasserstoffatome sowieso in einem vollständig ionisierten Plasma, also spielt die Abstoßung durch die Elektronenhülle keine Rolle mehr. Aber selbst dann ist es nur durch den Tunneleffekt möglich, dass eine aufrechterhaltende Fusionsreaktion zustande kommt. Um die nötige Aktivierungsenergie bei einer Wasserstoffbombe zu bekommen, wird dazu erstmal eine Kernspaltung (also eine "normale" Atombombe) gezündet und einem Fusionsreaktor des Tokamak Designs, wird das mehrere Millionen °C heiße Plasma durch ein Magnetfeld erzeugt und an der Stelle gehalten. Selbst wenn es "irgendwie" möglich wäre, eine Proton-Proton-Reaktion quasi bei Zimmertemperatur (oder ein paar hundert grad darüber), also "kalt" ablaufen zu lassen, hätte man noch das Problem, dass auch bei der Nutzbarmachung von "heißen" Fusionsreaktoren auftritt: ca 80% der freiwerdenden Energie ist nämlich kinetische Energie des entstehenden Neutrons, also Neutronenstrahlung. Gerade letztere scheint aber bei Versuchen wie die von Fleischmann und Pons gänzlich zu fehlen (Punkt 2). Außerdem müsste unter der Vielzahl der Reaktionen auch Wasserstoff zu Deuterium Reaktion wie $\rm{{}^1H + {}^1H \to {}^2H + e^+} + {\nu}_e$ ablaufen. Bei dieser Reaktion entsteht ein Positron, welches sehr schnell mit einem Elektron annihiliert wird. Dadurch enstehen zwei Photonen mit der charakteristischen Energie von $\rm{0{,}511~{MeV}}$. Diese Gammastrahlung fehlt aber ebenfalls (Punkt 3).
Aus theoretischer Sicht ist eine "kalte" Fusion also Humbug.
Was ist aber mit der vielzahl der Publikationen die "überschüßige Energie" und sogar Transmutationsprodukte in derartigen Zellen gemessen haben? Sind das nur falsch positive Ergebnisse oder gar Betrug? Was veranlasst die Zawodny von der NASA Langley zu solchen Aussagen:
(Quelle: youtube ; Originalvideo im NASA technology gateway)
Zawodny nennt die Antwort schon im Video: Neutroneneinfang. Die Theorie auf die sich Zawodny bezieht und zu der es am CERN im März ein Kolloquium gab, ist die Widom-Larson Theorie die hier im folgenden erklärt werden soll.
2. Die Widom-Larson-Theorie
Die Quellen auf die sich folgender Abschnitt beziehen sind:
(Fachkundige seien auch gleich auf diese Publikation verwießen, da folgender Abschnitt Grundlagen abhandelt und Details ignoriert)
1.) THE EUROPEAN PHYSICAL JOURNAL C Volume 46, Number 1, 107-111
"Widom, Larson - Ultra low momentum neutron catalyzed nuclear reactions on metallic hydride surfaces"
(arXiv:cond-mat/0505026v1)
2.) PRAMANA Vol. 75, No. 4 pp. 617:
"Srivastava, Widom, Larsen - A primer for electroweak induced low-energy nuclear reactions"
(arXiv:0810.0159v1)
2.1. Entstehung des Neutrons
Erstmal vorab zum Neutron: Ein Neutron ist ein ziemlich instabiles Teilchen. Ein freies (also außerhalb eines Atomkerns befindliches) Neutron hat eine Halbwertszeit von gerade mal 14 Minuten. Dabei zerfällt das Neutron in ein Proton, ein Elektron und ein Antineutrino:
$$
\mathrm{n\to p + e^-} + \bar{\nu}_e
$$
Nun passiert das aber nicht nur bei freien Neutronen, sondern auch bei Neutronen in bestimmten instabilen Atomkernen. Ein Beispiel wäre etwa das Nickel Isotop $\mathrm{^{63}Ni}$, das mit einer Halbwertszeit von 100 Jahren in das Kupferisotop $\mathrm{^{63}Cu}$ zerfällt. Ein Neutron aus dem Kern zerfällt unter β-Strahlung zu einem Proton. Dabei ändert sich die Massezahl nicht, aber das Element wird durch die Protonenanzahl zu einem anderen transmutiert:
$$
^{63}_{28}\rm{Ni} \to {^{63}_{29}\rm{Cu} + \rm{e}^-} + \bar{\nu}_e
$$
Nun geht dieser Prozess aber auch "andersherum":
$$
\rm{p} + \rm{e}^- \to \rm{n} + {\nu}_e
$$
Ein Proton fängt ein Elektron ein und es entsteht ein Neutron und ein Neutrino. Diesen "inverse β-Zerfall" bezeichnet man auch als Elektroneneinfang oder ε-Zerfall. Das sind "known physics" und ist bisher nichts besonderes. Der Knackpunkt bei dieser Geschichte ist die Seltenheit des Elektroneneinfang. Bei einem Proton passiert das nicht "einfach so". Im Folgenden soll schematisch an einem Proton die benötigte Energie für einen Elktroneneinfang berechnet werden.
Das Elektron hat die Ruhemasse $\rm{0,510~MeV/c^2}$, ein Neutron $\rm{939,5~MeV/c^2}$ und ein Proton $\rm{ 938,2~MeV/c^2}$. Die Differenz der Ruhemassen zwischen Proton und Neutron beträgt etwa $\rm{1,3~MeV/c^2}$ und die Ruhemasse von Proton und einem Neutron zusammen mit einem Elektron beträgt also $\rm{0,8~MeV/c^2}$. Für die Umwandlung eines Protons und Elektrons in ein Neutron brauchen wir also Energie. Für Energien im MeV Bereich reicht aber "Zimmertemperatur" bei weitem nicht aus. Ein Teilchen eine ideales Gas hat bei 20°C gerade mal eine mittlere kinetische Energie von:
$$
E_{\rm{kin}} = \frac{3}{2} \cdot 8{,}62 \cdot 10^{-5}~\rm{\frac{eV}{K}} \cdot 293,15~{\rm K} = 0{,}038~\rm{eV}
$$
Legt man nun in so einer $\rm{{Ni}{-}{H}}$ Zelle eine Spannung von etwa 100V, so ergibt sich für ein Elektron schematisch (Gleichung für Vakuum) gerade mal eine Kinetische Energie von:
$$
E_{\rm{kin}} = e \cdot U = 100~\rm{eV}
$$
Wie also auf die benötigte Energie in derartigen Versuchen kommen?
Laut Widom und Larsen sollen kollektive Effekte dazu führen, dass einzelne Elektronen die benötigten Energien erreichen.
Dazu werfen wir einen Blick auf die Schrödinger Gleichung. Diese Gleichung benötigt man für die Dynamik von quantenmechanischen Teilchen. Also etwa die Bewegung eines Elektrons. Was aber, wenn man die Bewegung von mehreren Teilchen berechnen will. Bei einem so einfachen Teilchen wie einem Wasserstoffmolekül haben wir bereits 4 Teilchen (2 Protonen und 2 Elektronen) und bereits dann ist eine analytische (also exakte) Lösung nicht mehr möglich. Das ganze lässt sich mit dem Dreikörperproblem aus der Astronomie vergleichen.
Wenn keine genauen Lösungen mehr möglich sind, dann beginnen die Mathematiker/Physiker mit "schätzen". Solche numerischen Näherungslösungen haben aber nicht zwangsläufig was mit rumraten zu tun. Ein sehr anschauliches Beispiel wie man etwa die Nullstelle einer Funktion numerisch Lösen kann bietet das Newton-Verfahren.
Kommen wir aber zurück zu unserem Wasserstoffmolekül. Um die Schrödingergleichung für diese Teilchen zu lösen können wir auf die Born-Oppenheimer-Approximation zurückgreifen. Die Idee von Born und Oppenheimer war vereinfacht formuliert folgende: Die Protonen und Neutronen mit ihrer Masse von fast $1000 \rm{MeV/c^2}$ sind deutlich träger als das leichte Elektron mit seiner Masse von gerade mal $ 0{,}5 \rm{MeV/c^2}$. Aus diesem Grund kann man den Atomkern als quasi ruhend annehmen. Dadurch wird die Gleichung dann lösbar.
Widom und Larsen gehen nun davon aus, dass es bei LENR einen lokalen Zusammenbruch der Born-Oppenheimer Approximation gibt und kollektive Effekte zu einer Masserenormierung einzelner Elektronen führen. Was heißt das im Klartext?!
Schematisch erklärt soll folgendes passieren: Die Atomkerne sind nicht ganz so in Ruhe, wie man das gerne zum Berechnen hätte, sondern schwingen ganz leicht. In einzelnen Fällen "schaukeln sich diese Schwingungen hoch". Durch diese kollektive Effekte sollen nun einzelne Elektronen eine Masserenormierung (eng.) auf die benötigte Masse erfahren.
Oben habe ich geschrieben, dass die Widom-Larson Theorie keine "neue Physik" benötigt. Die Born-Oppenheimer Approximation gehört aber auch zur "etablierten Physik". Handelt es sich hier also doch um "neue Physik". Nein, denn wie erwähnt ist die Born-Oppenheimer Approximation nur eine idealisierte Schätzung und dass diese verletzt werden kann, wurde schon experimentell gezeigt:
$$
\mathrm{n\to p + e^-} + \bar{\nu}_e
$$
Nun passiert das aber nicht nur bei freien Neutronen, sondern auch bei Neutronen in bestimmten instabilen Atomkernen. Ein Beispiel wäre etwa das Nickel Isotop $\mathrm{^{63}Ni}$, das mit einer Halbwertszeit von 100 Jahren in das Kupferisotop $\mathrm{^{63}Cu}$ zerfällt. Ein Neutron aus dem Kern zerfällt unter β-Strahlung zu einem Proton. Dabei ändert sich die Massezahl nicht, aber das Element wird durch die Protonenanzahl zu einem anderen transmutiert:
$$
^{63}_{28}\rm{Ni} \to {^{63}_{29}\rm{Cu} + \rm{e}^-} + \bar{\nu}_e
$$
Nun geht dieser Prozess aber auch "andersherum":
$$
\rm{p} + \rm{e}^- \to \rm{n} + {\nu}_e
$$
Ein Proton fängt ein Elektron ein und es entsteht ein Neutron und ein Neutrino. Diesen "inverse β-Zerfall" bezeichnet man auch als Elektroneneinfang oder ε-Zerfall. Das sind "known physics" und ist bisher nichts besonderes. Der Knackpunkt bei dieser Geschichte ist die Seltenheit des Elektroneneinfang. Bei einem Proton passiert das nicht "einfach so". Im Folgenden soll schematisch an einem Proton die benötigte Energie für einen Elktroneneinfang berechnet werden.
Das Elektron hat die Ruhemasse $\rm{0,510~MeV/c^2}$, ein Neutron $\rm{939,5~MeV/c^2}$ und ein Proton $\rm{ 938,2~MeV/c^2}$. Die Differenz der Ruhemassen zwischen Proton und Neutron beträgt etwa $\rm{1,3~MeV/c^2}$ und die Ruhemasse von Proton und einem Neutron zusammen mit einem Elektron beträgt also $\rm{0,8~MeV/c^2}$. Für die Umwandlung eines Protons und Elektrons in ein Neutron brauchen wir also Energie. Für Energien im MeV Bereich reicht aber "Zimmertemperatur" bei weitem nicht aus. Ein Teilchen eine ideales Gas hat bei 20°C gerade mal eine mittlere kinetische Energie von:
$$
E_{\rm{kin}} = \frac{3}{2} \cdot 8{,}62 \cdot 10^{-5}~\rm{\frac{eV}{K}} \cdot 293,15~{\rm K} = 0{,}038~\rm{eV}
$$
Legt man nun in so einer $\rm{{Ni}{-}{H}}$ Zelle eine Spannung von etwa 100V, so ergibt sich für ein Elektron schematisch (Gleichung für Vakuum) gerade mal eine Kinetische Energie von:
$$
E_{\rm{kin}} = e \cdot U = 100~\rm{eV}
$$
Wie also auf die benötigte Energie in derartigen Versuchen kommen?
Laut Widom und Larsen sollen kollektive Effekte dazu führen, dass einzelne Elektronen die benötigten Energien erreichen.
Dazu werfen wir einen Blick auf die Schrödinger Gleichung. Diese Gleichung benötigt man für die Dynamik von quantenmechanischen Teilchen. Also etwa die Bewegung eines Elektrons. Was aber, wenn man die Bewegung von mehreren Teilchen berechnen will. Bei einem so einfachen Teilchen wie einem Wasserstoffmolekül haben wir bereits 4 Teilchen (2 Protonen und 2 Elektronen) und bereits dann ist eine analytische (also exakte) Lösung nicht mehr möglich. Das ganze lässt sich mit dem Dreikörperproblem aus der Astronomie vergleichen.
Wenn keine genauen Lösungen mehr möglich sind, dann beginnen die Mathematiker/Physiker mit "schätzen". Solche numerischen Näherungslösungen haben aber nicht zwangsläufig was mit rumraten zu tun. Ein sehr anschauliches Beispiel wie man etwa die Nullstelle einer Funktion numerisch Lösen kann bietet das Newton-Verfahren.
Kommen wir aber zurück zu unserem Wasserstoffmolekül. Um die Schrödingergleichung für diese Teilchen zu lösen können wir auf die Born-Oppenheimer-Approximation zurückgreifen. Die Idee von Born und Oppenheimer war vereinfacht formuliert folgende: Die Protonen und Neutronen mit ihrer Masse von fast $1000 \rm{MeV/c^2}$ sind deutlich träger als das leichte Elektron mit seiner Masse von gerade mal $ 0{,}5 \rm{MeV/c^2}$. Aus diesem Grund kann man den Atomkern als quasi ruhend annehmen. Dadurch wird die Gleichung dann lösbar.
Widom und Larsen gehen nun davon aus, dass es bei LENR einen lokalen Zusammenbruch der Born-Oppenheimer Approximation gibt und kollektive Effekte zu einer Masserenormierung einzelner Elektronen führen. Was heißt das im Klartext?!
Schematisch erklärt soll folgendes passieren: Die Atomkerne sind nicht ganz so in Ruhe, wie man das gerne zum Berechnen hätte, sondern schwingen ganz leicht. In einzelnen Fällen "schaukeln sich diese Schwingungen hoch". Durch diese kollektive Effekte sollen nun einzelne Elektronen eine Masserenormierung (eng.) auf die benötigte Masse erfahren.
Oben habe ich geschrieben, dass die Widom-Larson Theorie keine "neue Physik" benötigt. Die Born-Oppenheimer Approximation gehört aber auch zur "etablierten Physik". Handelt es sich hier also doch um "neue Physik". Nein, denn wie erwähnt ist die Born-Oppenheimer Approximation nur eine idealisierte Schätzung und dass diese verletzt werden kann, wurde schon experimentell gezeigt:
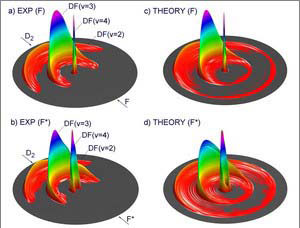 |
| (Quelle: nanowerk: A case where Born-Oppenheimer Approximation breaks down) |
Rechts sieht man die "theoretischen Werte" die sich aus der Born-Oppenheimer Näherung ergeben und links die experimentellen.
Im Zusammenhang mit der Theorie von Widom-Larson ist folgende Publikationen wichtig:
White et al. - Conversion of large-amplitude vibration to electron excitation at a metal surface. In dieser Publikation geht es darum, dass kollektive Effekte (Oszillation) auf Metalloberflächen dazu führen, dass lokal über 10.000 mal stärkere elektromagnetische Energie verfügbar ist. Machen wir dazu mal ein ganz schematische Rechnung zur Gesamtenergie:
$$ E = mc^2 + e \cdot U \\\\ = \mathrm {0{,}5~ MeV/c^2 \cdot c^2 + e \cdot 100~ V \cdot \mathit{10000} \\\\ = 0{,}5~ MeV + 1.000.000~eV = 1{,}5~ MeV} $$
Ich habe hier ganz schematisch die Gesamtenergie eines Elektrons durch die Masse und die Spannung berechnet (Temperatur nicht berücksichtigt). Die kinetische Energie durch die Spannung habe ich simpel mit dem Faktor 10000 der kollektiven Effekte multipliziert. Durch diese kollektiven Effekte könnte also die notwendige Energie für einen Elektroneneinfang vorhanden sein. Es könnte also aus einem Proton und Elektron ein Neutron entstehen.
In diesem Schritt passiert nun ein Neutroneneinfang. Das ist auch das was in einem Brutreaktor beim "brüten" von Plutonium passiert:
$$ \mathrm{^{238}_{\ 92}U \ + \ ^{1}_{0}n \ \longrightarrow\ ^{239}_{\ 92}U \ \xrightarrow {\beta^-} \ ^{239}_{\ 93}Np \ \xrightarrow {\beta^-} \ ^{239}_{\ 94}Pu} $$
Uran-238 nimmt ein Neutron auf, das instabile Isotop wird unter Beta-Zerfall zu Neptunium und unter weiterem Betazerfall zu Plutonium. Nun gibt es im Falle von Widom und Larsen einen gravierenden Unterschied zur Neutronenanlagerung wie sie etwa in einem Brutreaktor abläuft. Wenn man die Größe eines Atoms zu seinem Kern vergleicht, haben wir ein Verhältniss von einem Fussballplatz zu einem Stecknadelkopf. Schießt man jetzt einen anderen Stecknadelkopf durch den Fussballplatz, wird es sehr unwahrscheinlich, dass man den anderen Stecknadelkopf erwischt (nicht zu vergessen die riesigen Abstände der Fußballplätze zueinander). Deshalb brauchen Brutreaktoren eine große Neutronenflussrate (nach dem Motto: irgendwann trifft man schon). Außerdem ist die Neutronenstrahlung sehr schädlich für organisches Material.
Wie ist das aber bei LENR (nach Widom-Larsen)? Da gibt es doch nur eine "Handvoll" Neutronen die durch einige wenige EM-Fluxe entstehen...?
Hier spielt wieder die Quantenmechanik eine große Rolle, denn die Neutronen die auf diese Weise entstehen haben kaum kinetische Energie. Sind also ultrakalt (vgl. Neutronen Klassifizierung.) Das besondere an den ULM Neutronen ist, dass sie "riesig" sind bzw das sie eine große De-Broglie-Wellenlänge haben. Es gilt:
$$ \lambda = \frac{h}{p}$$
Wobei $\lambda$ die Wellenlänge ist. $h$ das Plancksche Wirkungsquantum und $p$ der Impuls (eng. momentum). Ist nun der Impuls sehr klein wird die Wellenlänge sehr groß. Die Wellenlänge wird bei derart kalten Neutronen größer als 2nm (nm=Nanometer) während ein Atom bei "Zimmertemperatur" "nur" 0,1 nm klein ist. Das heißt jetzt quasi, dass der oben erwähnte Stecknadelkopf jetzt (weit) über 20 mal so groß wie ein Fussballfeld ist. Damit wird es mit dem Treffen einfacher.
Das heißt jetzt also, dass diese Neutronen nicht nur total leicht von den Atomkernen aufgenommen werden, sonder sogar so leicht aufgenommen werden, dass sie quasi keine Chance haben zu entkommen, es also quasi keine Neutronenstrahlung gibt. Somit braucht man also keine Unmengen an schnellen (und gefährlichen) Neutronen wie in einem Kernkraftwerk.
Von hier an ist die Energieerzeugung nur noch ein kleiner Schritt. Ein Beispiel findet sich in obigen Publikationen:
$${}^6_3\mathrm{Li} + n \to {}^7_3\mathrm{Li} \\\\
{}^7_3\mathrm{Li} + n \to {}^8_3\mathrm{Li} \\\\
{}^8_3\mathrm{Li} \to {}^8_4\mathrm{Be} + \mathrm{e}^- + \bar{\nu}_e \\\\
{}^8_4\mathrm{Be} \to {}^4_2\mathrm{He} + {}^4_2\mathrm{He}$$
Die gesamte freiwerdende Energie würde hier bei 26,9 MeV liegen. Nun gäbe es aber noch das Problem, dass einige Energie in Form von (schädlicher) Strahlung frei werden würde. Hier spielen aber wieder die renormierten Elektronen eine Rolle:
Die Umwandlung von hochenergetischen Photonen (Gamma/Röntgenstrahlung) in niedereenergetische Photonen (infrarot also Wärme) wird detailierter in arXiv:cond-mat/0509269v1 beschrieben. Dieser Teil der Theorie übersteigt meine eigenen Kenntnisse und ich kann die Behauptung nicht beurteilen. Hätte es aber damit seine Richtigkeit wäre dies unabhängig von der Energieerzeugung von großem Nutzen, da es sehr kostengünstigen Strahlungsschutz ermöglichen könnte (etwa in der Raumfahrt).
Die Entäuschung 1989 nach Fleischmann und Pons war groß. Die Ergebnisse waren nicht eindeutig reproduzierbar, die Kalorimetrie war schlampig, die Veröffentlichung vorschnell und selbst wenn der Effekt da war, war die erzeugte Energie für die Praxis zu gering. Weiterhin war die Behauptung einer Fusion bei Zimmertemperatur quasi Blasphemie. Das Feld hat sich aber entwickelt. Die Reproduzierbarkeit wurde erhöht, die Kalorimetrie verbessert und die Energieausbeute (leicht) erhöht. Es wäre durchaus möglich, dass es sich um falsch positive Ergebnisse handelt. Betrachtet man aber das mögliche Potential, das in dieser Technologie steckt, so sollte man sich zumindest die Mühe machen, den Fehler zu suchen, denn wäre es kein Fehler, könnte die Lösung der Energieprobleme verschenkt worden sein.
Weiterhin gibt es mit der Widom und Larsen Theorie eine sehr elegante Erklärung für das Phänomen. Abgesehen davon können mit dieser Theorie bestimmte, bisher unverstandenen Phänomene der Natur - nämlich die Entstehung von Neutronen in Blitzen und die Hitze und hochenergetischen Teilchen in der Sonnenkorona - erklärt werden. Desweiteren sind theoretische Vorhersagen wie die Gammaabschirmung experimentell überprüfbar.
In den letzten Jahren hat das Thema immer mehr Intresse innerhalb der wissenschaftlichen Gemeinde gefunden und ich hoffe, dass es so weiter geht.
Im Zusammenhang mit der Theorie von Widom-Larson ist folgende Publikationen wichtig:
White et al. - Conversion of large-amplitude vibration to electron excitation at a metal surface. In dieser Publikation geht es darum, dass kollektive Effekte (Oszillation) auf Metalloberflächen dazu führen, dass lokal über 10.000 mal stärkere elektromagnetische Energie verfügbar ist. Machen wir dazu mal ein ganz schematische Rechnung zur Gesamtenergie:
$$ E = mc^2 + e \cdot U \\\\ = \mathrm {0{,}5~ MeV/c^2 \cdot c^2 + e \cdot 100~ V \cdot \mathit{10000} \\\\ = 0{,}5~ MeV + 1.000.000~eV = 1{,}5~ MeV} $$
Ich habe hier ganz schematisch die Gesamtenergie eines Elektrons durch die Masse und die Spannung berechnet (Temperatur nicht berücksichtigt). Die kinetische Energie durch die Spannung habe ich simpel mit dem Faktor 10000 der kollektiven Effekte multipliziert. Durch diese kollektiven Effekte könnte also die notwendige Energie für einen Elektroneneinfang vorhanden sein. Es könnte also aus einem Proton und Elektron ein Neutron entstehen.
2.2 Einfang des ULM-Neutron
In diesem Schritt passiert nun ein Neutroneneinfang. Das ist auch das was in einem Brutreaktor beim "brüten" von Plutonium passiert:
$$ \mathrm{^{238}_{\ 92}U \ + \ ^{1}_{0}n \ \longrightarrow\ ^{239}_{\ 92}U \ \xrightarrow {\beta^-} \ ^{239}_{\ 93}Np \ \xrightarrow {\beta^-} \ ^{239}_{\ 94}Pu} $$
Uran-238 nimmt ein Neutron auf, das instabile Isotop wird unter Beta-Zerfall zu Neptunium und unter weiterem Betazerfall zu Plutonium. Nun gibt es im Falle von Widom und Larsen einen gravierenden Unterschied zur Neutronenanlagerung wie sie etwa in einem Brutreaktor abläuft. Wenn man die Größe eines Atoms zu seinem Kern vergleicht, haben wir ein Verhältniss von einem Fussballplatz zu einem Stecknadelkopf. Schießt man jetzt einen anderen Stecknadelkopf durch den Fussballplatz, wird es sehr unwahrscheinlich, dass man den anderen Stecknadelkopf erwischt (nicht zu vergessen die riesigen Abstände der Fußballplätze zueinander). Deshalb brauchen Brutreaktoren eine große Neutronenflussrate (nach dem Motto: irgendwann trifft man schon). Außerdem ist die Neutronenstrahlung sehr schädlich für organisches Material.
Wie ist das aber bei LENR (nach Widom-Larsen)? Da gibt es doch nur eine "Handvoll" Neutronen die durch einige wenige EM-Fluxe entstehen...?
Hier spielt wieder die Quantenmechanik eine große Rolle, denn die Neutronen die auf diese Weise entstehen haben kaum kinetische Energie. Sind also ultrakalt (vgl. Neutronen Klassifizierung.) Das besondere an den ULM Neutronen ist, dass sie "riesig" sind bzw das sie eine große De-Broglie-Wellenlänge haben. Es gilt:
$$ \lambda = \frac{h}{p}$$
Wobei $\lambda$ die Wellenlänge ist. $h$ das Plancksche Wirkungsquantum und $p$ der Impuls (eng. momentum). Ist nun der Impuls sehr klein wird die Wellenlänge sehr groß. Die Wellenlänge wird bei derart kalten Neutronen größer als 2nm (nm=Nanometer) während ein Atom bei "Zimmertemperatur" "nur" 0,1 nm klein ist. Das heißt jetzt quasi, dass der oben erwähnte Stecknadelkopf jetzt (weit) über 20 mal so groß wie ein Fussballfeld ist. Damit wird es mit dem Treffen einfacher.
Das heißt jetzt also, dass diese Neutronen nicht nur total leicht von den Atomkernen aufgenommen werden, sonder sogar so leicht aufgenommen werden, dass sie quasi keine Chance haben zu entkommen, es also quasi keine Neutronenstrahlung gibt. Somit braucht man also keine Unmengen an schnellen (und gefährlichen) Neutronen wie in einem Kernkraftwerk.
Von hier an ist die Energieerzeugung nur noch ein kleiner Schritt. Ein Beispiel findet sich in obigen Publikationen:
$${}^6_3\mathrm{Li} + n \to {}^7_3\mathrm{Li} \\\\
{}^7_3\mathrm{Li} + n \to {}^8_3\mathrm{Li} \\\\
{}^8_3\mathrm{Li} \to {}^8_4\mathrm{Be} + \mathrm{e}^- + \bar{\nu}_e \\\\
{}^8_4\mathrm{Be} \to {}^4_2\mathrm{He} + {}^4_2\mathrm{He}$$
Die gesamte freiwerdende Energie würde hier bei 26,9 MeV liegen. Nun gäbe es aber noch das Problem, dass einige Energie in Form von (schädlicher) Strahlung frei werden würde. Hier spielen aber wieder die renormierten Elektronen eine Rolle:
"The observed electromagnetic radiation from the surface heavy electrons will be confined essentially to low-energy photons reaching up to soft X-rays with practically no MeV range photon's being radiated because the mean free path of the produced γ-rays in the few MeV range would be very short, about a few Angstroms. To recapitulate: The surface charge oscillation plasmons provide enough collective energy for the production of heavy mass electrons which in turn lead to the production of low-momentum neutrons. Such neutrons get readily absorbed and their production dynamics produces their own neutrons and built-in γ-ray 'shields'." (Quelle: "Srivastava, Widom, Larsen - A primer for electroweak induced low-energy nuclear reactions")
Die Umwandlung von hochenergetischen Photonen (Gamma/Röntgenstrahlung) in niedereenergetische Photonen (infrarot also Wärme) wird detailierter in arXiv:cond-mat/0509269v1 beschrieben. Dieser Teil der Theorie übersteigt meine eigenen Kenntnisse und ich kann die Behauptung nicht beurteilen. Hätte es aber damit seine Richtigkeit wäre dies unabhängig von der Energieerzeugung von großem Nutzen, da es sehr kostengünstigen Strahlungsschutz ermöglichen könnte (etwa in der Raumfahrt).
3. Schlusswort
Die Entäuschung 1989 nach Fleischmann und Pons war groß. Die Ergebnisse waren nicht eindeutig reproduzierbar, die Kalorimetrie war schlampig, die Veröffentlichung vorschnell und selbst wenn der Effekt da war, war die erzeugte Energie für die Praxis zu gering. Weiterhin war die Behauptung einer Fusion bei Zimmertemperatur quasi Blasphemie. Das Feld hat sich aber entwickelt. Die Reproduzierbarkeit wurde erhöht, die Kalorimetrie verbessert und die Energieausbeute (leicht) erhöht. Es wäre durchaus möglich, dass es sich um falsch positive Ergebnisse handelt. Betrachtet man aber das mögliche Potential, das in dieser Technologie steckt, so sollte man sich zumindest die Mühe machen, den Fehler zu suchen, denn wäre es kein Fehler, könnte die Lösung der Energieprobleme verschenkt worden sein.
Weiterhin gibt es mit der Widom und Larsen Theorie eine sehr elegante Erklärung für das Phänomen. Abgesehen davon können mit dieser Theorie bestimmte, bisher unverstandenen Phänomene der Natur - nämlich die Entstehung von Neutronen in Blitzen und die Hitze und hochenergetischen Teilchen in der Sonnenkorona - erklärt werden. Desweiteren sind theoretische Vorhersagen wie die Gammaabschirmung experimentell überprüfbar.
In den letzten Jahren hat das Thema immer mehr Intresse innerhalb der wissenschaftlichen Gemeinde gefunden und ich hoffe, dass es so weiter geht.
Sollte das wirklich funzen, werden die entscheidenden Personen sehr schnell ermordet werden, wie alle zuvor, denen ähnliches gelungen war, nicht nur Tesla, Reich, Schauberger, alle von den USA fertig gemacht und faktisch ermordet.
AntwortenLöschenTesla war hinsichtlich Lobbyarbeit schlechter als Eddison, weshalb sich zuerst Eddison durchsetzte. Eigenartiger weise ist der Strom der aus meiner Steckdose kommt Wechselstrom und Leuchtstoffröhren liegen auch nicht irgendwo versteckt in Schubladen von Energiekonzernen. Was Reich und DeMeo angeht, ...hab reingeschaut und hab Kopfschmerzen von dem Müll bekommen, ... halt mich meinetwegen für ein leichtgläubiges Schäfchen, das nicht selber denken kann ...
AntwortenLöschenNoch was, wenn zum "fertig machen" und "faktisch ermorden" dazugehört, dass man eine physikalische Größe nach der Person benennt (Einheit der magnetische Flussdichte ist Tesla), ihn mit Ehrendoktorentitel überschüttet, ihm zig Patente gewährt und einen Mondkrater und Asteroiden nach ihm benennt, dann kann man das mit mir auch gern machen.
AntwortenLöschenNun, das Benennen von irgendwas nach Tesla waren sicher nicht die Vertreter der Hochfinanz in den USA.
AntwortenLöschenDa scheint Ihnen noch reichtlich Verständnis für Zusammenhänge und vor allem für Hintergründe zu fehlen, wenn Sie die Verbrechen an diesen europäischen Größen durch die US-Hochfinanz verharmlosen wollen.
Welche Verbrechen wären das denn? Etwa die von Westinghouse und General Electric die den Wechselstrom nach Teslas Patenten gegenüber Eddison durchsetzten. Oder die Beratersummen die Westinghouse ihm später zahlte? Oder etwa die Finanzierung des Wardenclyffe Tower durch J P Morgan (unter falschen Angaben Teslas gegenüber JP Morgan)? Der arme Mann war zeitweise so reich, dass er sein Krawatten nach dem ersten tragen weggeworfen hat.
AntwortenLöschenedison zog mit elektrodrähten durchs land und hat vor publikum tiere getötet, um tesla zu diffarmieren und die gefährlichkeit von wechselstrom im haushalt herauszustreichen. natürlich wäre das bei gleichstrom nicht besser gewesen. als dank dafür hat die us regierung EDISON gebeten, ihnen wechselstrom vorzuführen, worauf sie ihm schliesslich den auftrag für den ersten elektrischen stuhl gaben. sicher hat sich teslas idee durchgesetzt aber EDISON hat sich damit bis zu seinem tode dumm und dämlich verdient. tesla war gegen ende der seltsame visionär, dem man im zuge der globalen unruhe dann lieber die gelder strich, bevor es interessant wurde. edison hingegen wurde sinnlos glorifiziert, in die usa geschichte zentral integriert und heute lernt jedes kind, dass edison all das erfunden hat. zumindest dort. so läuft das mit ideen, patenten und erfindern. hochfinanz ist so ein nichtssagendes wort aber letztendlich kann im kapitalismus sich nur das durchsetzen, was am meisten geld einbringt und nicht automatisch die beste technik. (die glühbirne und ihre künstlich verkürzte lebensdauer ist hier ein gutes beispiel.) und natürlich würden diese menschen über leichen gehen, um ihre implizierten gewinne nicht zu gefährden. man gucke sich nur zB die äh... viralen marketingstrategien der tabak- und atomlobby im vergleich an.
LöschenDanke für diese vorzügliche Zusammenfassung.
AntwortenLöschenSollte dies wirklich zutreffen:
"Dies ist der Blog eines unter notorischer Neugier leidenden Philosophiestudenten, .."
dann könnte man ja ein Philosophiestudium fast empfehlen!
Grüße!
Ein wunderbarer und informativer Artikel, danke Melethron. Zu den obigen Kommentaren kann ich nur sagen: Don't feed the Trolls.
AntwortenLöschenDanke für das Lob. Widom Larson rückt mittlerweile immer mehr in den Blick des Mainstreams. So etwa in einem aktuellen Artikel im Discover Magazin: http://in.zinio.com/sitemap/ScienceTech-magazines/Discover/Nov-12/cat1960026/is-416237221/pg-13
LöschenHey, auch Danke für den super Artikel.
AntwortenLöschenFreue mich auch, dass Sie offen genug sind, auf Kommentare einzugehen*, die Schauberger et al erwähnen, und dabei differenziert und sachlich bleiben. *(Zumindest am Anfang, irgendwann wird's dann wohl doch zu off-topic).
Habe letztens gelesen, dass "Troll" eine letztlich entmenschlichend gemeinte Bezeichnung ist. Mir fiel's wie Schuppen von den Augen und es war fortan offensichtlich - auch dass so ein Begriff nur zur Extremisierung durch Ausgrenzungs- (sogar aus der Menschlichkeit)-Schmerz beiträgt.
Die Leute hier wollten auch nicht klassisch "trollen", sondern ihre ehrliche Meinung vortragen.
Anyway, wenn die Theorie von mehr Menschen verstanden wird, wozu Sie ja beitragen, dann könnte das Ganze im Falle eines Falles auch nicht mehr so leicht unter den Teppich gekehrt werden.
Ich finde Troll nicht entmenschlichend. Das kommt ja nicht vom Troll sonder von "to troll" (angeln). Troll bezieht sich mehr auf die Handlung, als auf die Person. Ich verstehe diesen Begriff nicht negativ und trolle eigentlich selber gerne mal.
LöschenAbgesehen davon wird Kalte Fusion nicht unter den Tisch gekehrt. Dass Kalte Fusion als junk science gilt, hat auch mit der vorschnellen Veröffentlichung zu tun. Druck der Uni aus PR euphorie etc. Anschließend wurde es in einer Art Selbstläufer zum Inbegriff der Junk Science. Die Hot Fusion Forscher sind selbstverständlich ziemlich "skeptisch" und von daher kommt es kaum zu einer neutralen Betrachtung, aber das ist das übliche Konkurenzdenken. Eine Verschwörung seh ich da aber nicht. Abgesehen davon sehen sich die Vertreter der Disziplin von der Marktreife noch über 10 Jahre entfernt (Quelle: Abschlussdiskussion ICCF 2012). Mit 10 Watt in Form von Wärme ist noch keine Energierevolution ;-) .
Übrigens wollt ich mal noch in einem Update über das berichten: http://newenergytimes.com/v2/sr/WL/slides/20111125LatticeEnergyDoc.pdf
Hab zur Zeit aber irgendwie keinen Kopf für Artikel schreiben. Aber ein Update zu WL folgt.